Minilab 2: Future evolution of HMXBs

High mass X-ray binaries with black holes
Modifications to the template
Run your models
Limitations of MESA
Angular momentum losses
1. Copy the null routine for the hook
2. Locate and modify the original code
Extra work
References

High mass X-ray binaries with black holes

The objective of this lab will be to study the future evolution of X-ray binaries known to have black holes, for which we also have a well characterised orbital solution. The following table shows the properties of these systems that will be relevant to our models:

Name	$M_\mathrm{star}$ $[M_\odot]$	$M_\mathrm{BH}$ $[M_\odot]$	Period $[d]$	Reference
Cyg X-1	$40.6^{+7.7}_{-7.1}$	$21.2^{+2.2}_{-2.3}$	$5.60$	Miller-Jones et al. (2021)
LMC X-1	$31.79\pm3.67$	$10.9\pm1.4$	$3.91$	Orosz et al. (2009)
M33 X-7	$70.0\pm6.9$	$15.65\pm1.45$	$3.45$	Orosz et al. (2007)

HMXBs with orbital solutions that are known to host black holes.

All of these systems are expected to have started as a non-degenerate binary, where the progenitor of the black hole transferred mass to the star that is currently observed in the system. This potentially means that the star that is observed digresses from the evolution of a single star, and if we wanted to be fully consistent we would need to model the evolution of the system starting from two stars at the zero age main sequence. Here we will avoid this complication by approximating the star as a zero age main sequence star of the present-day mass, and we will also ignore the errors in the observations. So, for example, to model Cyg X-1 we will use the following in our inlist_project:

m1 = 40.6d0
m2 = 21.2d0
initial_period_in_days = 5.6d0

Here m1 corresponds to the mass of the star and m2 to the mass of the black hole, which me model as a point mass. The objective will be to model the three systems in the table above, study how binary interaction differs between them, and assess some of the limitations of the binary module.

Modifications to the template

We will start this minilab using the solution to minilab 1. Throughout the lab we will make use of mdot_scheme='Kolb'. Two small adjustements that we will need are the following

Set max_model_number=400 in inlist1. This is enough to model the systems until near-detachment. We will ignore the core helium burning phase.
Add Kipp_xaxis_name = 'star_age' and change History_Panels1_xaxis_name='star_age' in inlist1. Having properties shown against time instead of model number in pgstar will help understand the different timescales that come into play.

Did you have issues finishing minilab1? You can get a working copy of its solution here.

Run your models

Now, using the adjusted template, run all three simulations. Answer the following questions, and discuss them with those on your table. You can also spread out the work among your nearby colleagues:

How much does the mass transfer phase last compared to the total lifetime of the system (consider here only the time modeled within the max_model_number=400 constraint).
Do the evolution of these systems differ qualitatively from the one on minilab1?
Are all simulations running smoothly? Or are you running into numerical issues?

The last point in particular will be dealt with in the next section, so if you find everything is running smoothly be sure to double check!

Limitations of MESA

As you might have seen, two of the systems modeled runs into some issues (to put it lightly). Mass transfer rates go to very high values, approaching a solar mass per year. This points to some limitations within MESA, as the code models the donor star as a 1-dimensional object. For extreme mass ratios, the shrinkage of the orbit as mass transfer proceeds becomes extreme enough that the star cannot adjust itself through mass loss to avoid extreme overflow. In such a case the donor would very likely engulf its companion, initiating a process of common-envelope evolution which is fundamentally 3-dimensional. MESA being a 1-dimensional code cannot deal with such a situation, but rather tries to keep modeling this evolutionary phase as a stable mass transfer event with an ever increasing mass transfer rate, which eventually leads to numerical problems.

Although there are ways to approximate a common-envelope phase with MESA, here we wish to simply construct a physical criteria to identify when an unstable mass transfer phase could start, and terminate the evolution at that stage. For this purpose we will consider the thermal and dynamical timescales of the star:

\tau_\mathrm{thermal}=\frac{GM^2}{RL},\quad \tau_\mathrm{dynamical}=\frac{1}{\sqrt{G\langle \rho\rangle}}

From these one can define characteristic mass transfer rates:

\dot{M}_\mathrm{thermal}=\frac{M}{\tau_\mathrm{thermal}}\quad \dot{M}_\mathrm{dynamical}=\frac{M}{\tau_\mathrm{dynamical}}

As a criteria to test for unstable mass transfer we will check at the end of each timestep if the mass transfer $\dot{M}_\mathrm{transfer}$ exceeds significantly the thermal rate. This is indicative of the donor approaching a near-adiabatic behavior, leading to runaway overflow. In particular, we will require that $\dot{M}_\mathrm{transfer}>100 \dot{M}_\mathrm{thermal}$ to terminate the simulation.

Implement this check in extras_binary_finish_step. Use the following pointers to do so:

You can use the defined constant standard_cgrav. Compute both $\dot{M}_\mathrm{thermal}$ and $\dot{M}_\mathrm{dynamical}$ and print their values out, to turn them from cgs units to solar masses per year, you can use the constants Msun and secyer.
The mass transfer rate is contained in b% mtransfer_rate. Bear in mind that it is defined as negative.
Setting extras_binary_finish_step = terminate within the subroutine will terminate your simulation.
Whenever you terminate a simulation in this way, it is ideal to print a message so the run does not just silently stop.

integer function extras_binary_finish_step(binary_id)
   type (binary_info), pointer :: b
   integer, intent(in) :: binary_id
   integer :: ierr
   real(dp) :: mdot_th, mdot_dyn, avg_rho
   call binary_ptr(binary_id, b, ierr)
   if (ierr /= 0) then ! failure in  binary_ptr
      return
   end if  
   extras_binary_finish_step = keep_going

   mdot_th = b% m(1)/(standard_cgrav*(b% m(1))**2/(b% s1% L(1)*b% r(1)))

   avg_rho = b% m(1)/(4d0/3d0*(b% r(1))**3)
   mdot_dyn = b% m(1)/(1/sqrt(standard_cgrav*avg_rho))

   write(*,*) "check mdots", mdot_th/Msun*secyer, mdot_dyn/Msun*secyer
   if (abs(b% mtransfer_rate)>100d0*mdot_th) then
       write(*,*) "Finish simulation due to high mass transfer rate"
       extras_binary_finish_step = terminate
   end if

   
end function extras_binary_finish_step

After making these changes re-run the model that had issues, and see if it triggers the condition. Also, see how the thermal timescale compares to the dynamical one.

Having physical termination conditions to capture regions where MESA cannot properly model an evolutionary phase can be very valuable. It helps avoid the production of spurious results, and also avoids simulations from getting stuck into situations where timesteps become extremely small and simulations could in principle run for years without completing. This can be a big issue when running a large number of simulations in a cluster, potentially leading to a significant waste of resources. Ensuring we don't have pointless simulations running helps our carbon-footprint so we feel less guilty about travelling so much!

Angular momentum losses

In the simulations we have done so far mass transfer is highly non-conservative. To model orbital evolution, it is assumed that the material that is removed carries the same specific orbital angular momentum as the compact object. However, during the mass transfer process material can be potentially ejected from the outer Lagrangian points instead, as illustrated in the following figure:

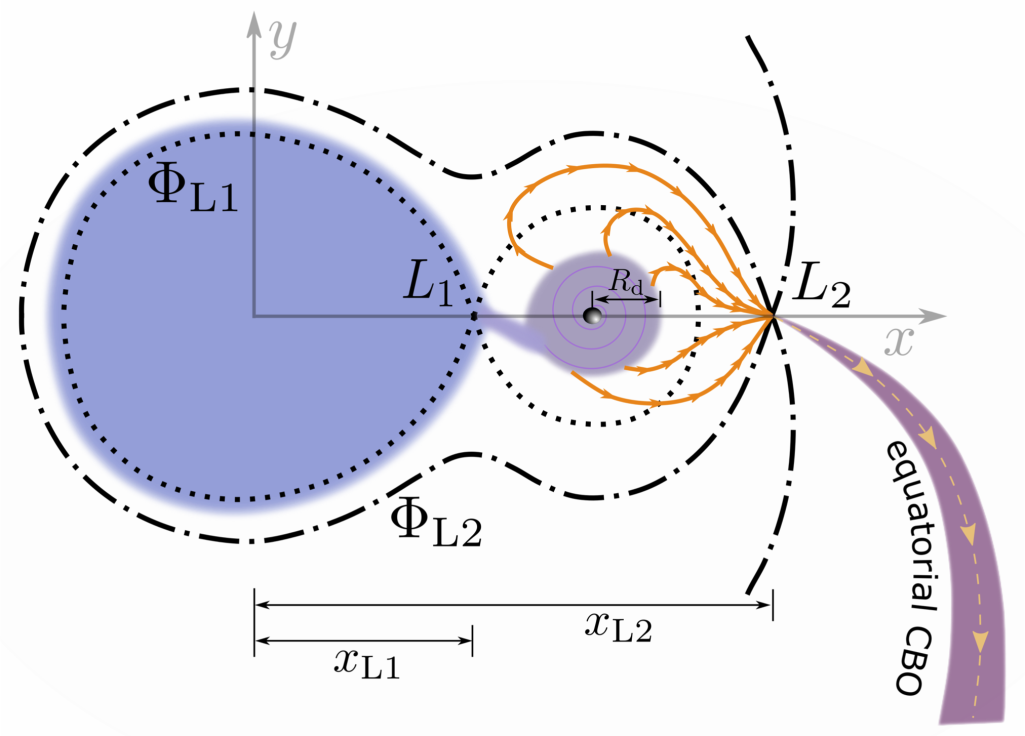
Ejection of material from the accretion disk towards the second Lagrangian point. Image from \cite{Lu+22}, CBO stands for circumbinary outflow. — Ejection of material from the accretion disk towards the second Lagrangian point. Image from Lu et al. (2022), CBO stands for circumbinary outflow.

We will not study here the different physical processes that can lead to such outflows, but just consider how they could impact orbital evolution. As the outer Lagrangian points are farther away from the center of mass of the system than the accreting star, the orbital angular momentum of material that co-rotates with them is higher. Material that is ejected through the outer Lagrangian points is then expected to increase the loss of orbital angular momentum, leading to smaller orbital separations as mass transfer proceeds.

For simplicity, we will assume a simple boost of a factor of 3 compared to the standard amount of angular momentum lost due to mass loss. This will be done using an other hook in run_binary_extras. Here we will go step-by-step on how one would implement this, also dealing with how the original implementation that we want to modify can be localized within the MESA source code.

Copy the null routine for the hook

The hook we will use is other_jdot_ml. Start by including use_other_jdot_ml = .true. in the binary_controls section of your inlist_project. If you just do this, the code will use a null subroutine to compute the angular momentum loss, which just sets it to zero. This is a placeholder that you need to replace with the subroutine you want to use. For this, do the following:

Look up in the files in $MESA_DIR/binary/other for the place where this null subroutine is defined, and copy it to your run_binary_extras.
Give the copied subroutine a name of your liking.
Make MESA aware of this subroutine in your run_binary_extras by pointing to it in extras_binary_controls (the following assumes you named this subroutine my_jdot_ml):

b% other_jdot_ml => my_jdot_ml

After doing this compile your work directory to verify there are no issues up to this stage.

Locate and modify the original code

Now we want to locate the place within MESA where the angular momentum loss is computed, and modify it accordingly in our hook. Start in a terminal by going to the folder where the binary module is located, and use the grep command to find where the code we are looking for is. We can focus on the $MESA_DIR/binary/private folder which contains the relevant files of the binary module, and look for jdot_ml.

cd $MESA_DIR/binary
grep -n -r "jdot_ml" private/*

The -n argument for grep will provide the line number. The -r command will recursively look into folders, it is not necessary in this particular case, but it is useful when trying to locate things in a wider range of locations. The outcome of this command should look like the following:

private/binary_ce.f90:262:         b% jdot_ml = 0d0
private/binary_ctrls_io.f90:145:         do_jdot_ml, &
private/binary_ctrls_io.f90:223:         use_other_jdot_ml, &
private/binary_ctrls_io.f90:495:         b% do_jdot_ml = do_jdot_ml
private/binary_ctrls_io.f90:573:         b% use_other_jdot_ml = use_other_jdot_ml
private/binary_ctrls_io.f90:685:         do_jdot_ml = b% do_jdot_ml
private/binary_ctrls_io.f90:759:         use_other_jdot_ml = b% use_other_jdot_ml
private/binary_do_one_utils.f90:368:            b% jdot_ml, &
private/binary_evolve.f90:378:            write(*,*) "jdot, jdot_mb, jdot_gr, jdot_ml:", b% jdot, b% jdot_mb, b% jdot_gr, b% jdot_ml
private/binary_history.f90:609:            case(bh_jdot_ml)
private/binary_history.f90:610:               val = b% jdot_ml
private/binary_jdot.f90:54:         if (.not. b% do_jdot_ml) then
private/binary_jdot.f90:55:             b% jdot_ml = 0d0
private/binary_jdot.f90:56:         else if (.not. b% use_other_jdot_ml) then
private/binary_jdot.f90:57:             call default_jdot_ml(b% binary_id, ierr)
private/binary_jdot.f90:59:             call b% other_jdot_ml(b% binary_id, ierr)
private/binary_jdot.f90:96:         get_jdot = (b% jdot_mb + b% jdot_gr + b% jdot_ml + b% jdot_missing_wind + &
private/binary_jdot.f90:119:      subroutine default_jdot_ml(binary_id, ierr)
private/binary_jdot.f90:131:         b% jdot_ml = (b% mdot_system_transfer(b% d_i) + b% mdot_system_wind(b% d_i))*&
private/binary_jdot.f90:135:         b% jdot_ml = b% jdot_ml + (b% mdot_system_transfer(b% a_i) + b% mdot_system_wind(b% a_i))*&
private/binary_jdot.f90:139:         b% jdot_ml = b% jdot_ml + b% mdot_system_cct * b% mass_transfer_gamma * &
private/binary_jdot.f90:141:      end subroutine default_jdot_ml
private/binary_private_def.f90:86:      integer, parameter :: bh_jdot_ml = bh_jdot_gr + 1
private/binary_private_def.f90:87:      integer, parameter :: bh_jdot_ls = bh_jdot_ml + 1
private/binary_private_def.f90:174:         binary_history_column_name(bh_jdot_ml) = 'jdot_ml'
private/run_binary_support.f90:180:         b% other_jdot_ml => null_other_jdot_ml

Using this information, locate the relevant subroutine and copy its contents into the custom subroutine in your run_binary_extras. Lookup the contribution from mass loss near the vicinity of the accretor and include a factor of 3 boost to it. Then compile your work directory before running a simulation.

I've had a non-negligible number of ocassions were I setup a hook but forget some important detail in the process like including use_other_jdot_ml in my inlists. I would recommend at first printing out a simple message from your hook subroutine to double-check that it is actually being used!

Rerun a case that was stable

With everything ready, go ahead and rerun one of the binary systems that underwent stable mass transfer. How does the evolution differ with the shift in angular momentum loss? If you have trouble implementing this hook, below you can find the implementation for it.

subroutine extras_binary_controls(binary_id, ierr)
   integer :: binary_id
   integer, intent(out) :: ierr
   type (binary_info), pointer :: b
   ierr = 0 

   call binary_ptr(binary_id, b, ierr)
   if (ierr /= 0) then
      write(*,*) 'failed in binary_ptr'
      return
   end if

   ! Set these function pointers to point to the functions you wish to use in
   ! your run_binary_extras. Any which are not set, default to a null_ version
   ! which does nothing.
   b% how_many_extra_binary_history_header_items => how_many_extra_binary_history_header_items
   b% data_for_extra_binary_history_header_items => data_for_extra_binary_history_header_items
   b% how_many_extra_binary_history_columns => how_many_extra_binary_history_columns
   b% data_for_extra_binary_history_columns => data_for_extra_binary_history_columns

   b% extras_binary_startup=> extras_binary_startup
   b% extras_binary_start_step=> extras_binary_start_step
   b% extras_binary_check_model=> extras_binary_check_model
   b% extras_binary_finish_step => extras_binary_finish_step
   b% extras_binary_after_evolve=> extras_binary_after_evolve

   b% other_jdot_ml => my_jdot_ml

   ! Once you have set the function pointers you want, then uncomment this (or set it in your star_job inlist)
   ! to disable the printed warning message,
    b% warn_binary_extra =.false.
   
end subroutine extras_binary_controls

subroutine my_jdot_ml(binary_id, ierr)
   integer, intent(in) :: binary_id
   integer, intent(out) :: ierr
   type (binary_info), pointer :: b
   ierr = 0 
   call binary_ptr(binary_id, b, ierr)
   if (ierr /= 0) then
      write(*,*) 'failed in binary_ptr'
      return
   end if
   !mass lost from vicinity of donor
   b% jdot_ml = (b% mdot_system_transfer(b% d_i) + b% mdot_system_wind(b% d_i))*&
       pow2(b% m(b% a_i)/(b% m(b% a_i)+b% m(b% d_i))*b% separation)*2*pi/b% period *&
       sqrt(1 - pow2(b% eccentricity))
   !mass lost from vicinity of accretor
   b% jdot_ml = b% jdot_ml + 3d0*(b% mdot_system_transfer(b% a_i) + b% mdot_system_wind(b% a_i))*&
       pow2(b% m(b% d_i)/(b% m(b% a_i)+b% m(b% d_i))*b% separation)*2*pi/b% period *&
       sqrt(1 - pow2(b% eccentricity))
   !mass lost from circumbinary coplanar toroid
   b% jdot_ml = b% jdot_ml + b% mdot_system_cct * b% mass_transfer_gamma * & 
       sqrt(standard_cgrav * (b% m(1) + b% m(2)) * b% separation)
end subroutine my_jdot_ml

Extra work

All done already! Then pat yourself in the back and try out the following. While implementing a boosted angular momentum loss we have just used a constant factor. A more physical approach would be to use the actual specific angular momentum of $L_2$ . To do this we need to determine the distance from the center of mass to the second Lagrangian point. The dimensionless roche potential of a system with masses $M_1$ and $M_2$ (from which we define the mass ratio $q=M_2/M_1$ ) is given by

\Phi=-\frac{1}{r} - q\left(\frac{1}{r'}-x\right)-\frac{1+q}{2}(x^2+y^2)

with

r = \sqrt{x^2+y^2+z^2}, \quad r' = \sqrt{(1-x)^2+y^2+z^2}.

The coordinates $x$ and $y$ here are within the orbital plane (see Figure above), while $z$ is the coordinate perpendicular to the orbital plane. The potential is normalized by $GM_1/a$ and distances are normalized by $a$ . The figure below shows the Roche potential for a mass ratio $q=0.5$ along the line joining both stars.

Roche potential along the line joining two stars in a binary system with $M_1/M_2=0.5$. The three peaks in the potential correspond to the Lagrangian points $L_1$, $L_2$ and $L_3$ in order of increasing $\Phi$. — Roche potential along the line joining two stars in a binary system with $M_1/M_2=0.5$ . The three peaks in the potential correspond to the Lagrangian points $L_1$ , $L_2$ and $L_3$ in order of increasing $\Phi$ .

From this, how would you proceed to compute the distance between $L_2$ and the center of mass of the binary system? Fully implementing this in your run_binary_extras can be a heavy task, so don't worry if you can't manage to finish it. Most relevant part is that you understand how this could be implemented.

References

Miller-Jones, James C. A., et al., Science, Volume 371, Issue 6533, pp. 1046-1049 (2021)
Orosz, Jerome A., et al., Nature, Volume 449, Issue 7164, pp. 872-875 (2007)
Orosz, Jerome A., et al., The Astrophysical Journal, Volume 697, Issue 1, pp. 573-591 (2009)
Lu, Wenbin ; Fuller, Jim ; Quataert, Eliot ; Bonnerot, Clément, eprint arXiv:2204.00847

CC BY-SA 4.0 Pablo Marchant. Last modified: August 09, 2022. Website built with Franklin.jl and the Julia programming language.